21. 알고리즘 - 분할 정복법 | 점화식
September 25, 2021
해당 포스트는 아래 수업들의 내용을 바탕으로 작성되었습니다.
- Youtube :
‘Chan-Su Shin’
- Professor : 신찬수 교수 (한국 외국어 대학교 컴퓨터 공학부)
1. 이전 항의 계수가 1인 점화식
지금까지 살펴본 분할 정복 알고리즘의 수행 시간은, 모두 T(n) 에 대한 점화식으로 표현되었다.
그리고, 이러한 점화식들은 알고리즘이 동작하는 방식에 따라서 여러 가지 형태를 띠었다.
- 물론, 지금까지의 수업에서는 이러한 점화식들을 모두 직접 전개하는 방식으로 풀어왔다.
- 하지만, 이번 수업에서는, 지금까지와는 다르게, 그림을 그려, 개념적으로 풀어볼 것이다.
1-1. 이진 탐색 알고리즘
첫 번째로 살펴볼 것은, 바로 이전 수업에서 살펴봤던 이진 탐색 알고리즘에 대한 점화식이다.
T(n) = T(n / 2) + c, T(1) = c재귀적인 관점 대신, ‘문제의 크기가 절반으로 줄어든다.’ 라는 직관적인 관점에서 살펴보자.
이 때, n 크기의 문제가 계속해서 (n / 2) 크기의 문제로 나뉘므로, n = 2^k 라고 가정할 것이다.
- 물론, 빅오 표기법의 특성상 결과는 같을 것이므로, n의 값이 무조건 2^k 일 필요는 없다.
- 하지만, n을 2로 k번 나누면 1이 되는 간단한 식을 유도하기 위해, 이렇게 가정하는 것이다.
그림을 그리면서 점화식을 풀면, 알고리즘의 동작 원리를 훨씬 더 직관적으로 확인할 수 있다.
n -> (n / 2) + c -> (n / 2^2) + c -> ... -> (n / 2^k) + c- n 크기의 문제가 (n / 2) 크기의 문제로 줄어들 때, 상수 횟수(c) 만큼의 연산이 추가된다.
- (n / 2) 크기의 문제가 다시 절반으로 줄어들 때도, 상수 횟수(c) 만큼의 연산이 추가된다.
- 문제의 크기를 계속 절반씩 줄여나가다 보면, 결국, 문제의 크기는 (n / 2^k) 이 될 것이다.
- 이 때, 위에서 한 가정에 따르면 n = 2^k 이므로, T(n / 2^k) = T(n / n) = T(1) = c 가 된다.
문제의 크기가 점화식의 일반항과 같아졌으니, 이제, 추가 연산의 횟수만 파악하면 된다.
n
↓
(n / 2) + c ┐
↓ │
(n / 2^2) + c │
↓ ├ k ┐
... │ │
↓ │ ├ (k + 1)
(n / 2^k) + c ┘ │
↓ │
c ────────────┘- 문제의 크기가 줄어든 횟수는 k번이므로, 상수 횟수(c) 의 추가 연산도 k번 수행된다.
- 따라서, T(n / 2^k) 의 수행 시간까지 고려하면, 전체 수행 시간은 c * (k + 1) 이 된다.
여기서, n = 2^k 의 양변에 로그를 취하면, k = log2(n) 이 되므로, T(n) = O(log n) 이 된다.
T(n) = c * (k + 1) = c * (log2(n) + 1) = O(log n)
↘ ↗
n = 2^k => k = log2(n)- 다시 말해, 이진 탐색 알고리즘은 log2(n) 번의 비교 연산을 통해 수행된다는 뜻이다.
- 앞에서부터 하나씩 비교해야 하는 상황이었다면, n번의 비교 연산이 필요했을 것이다.
- 하지만, 탐색 대상이 정렬된 상태라는 사실을 잘 이용해, 비교 횟수를 줄일 수 있었다.
1-2. Quick Select 알고리즘의 최선의 경우
이번에는, Quick Select 알고리즘의 최선의 경우(Best Case) 에 대한 점화식을 살펴보자.
T(n) = T(n / 2) + (c * n), T(1) = c, n = 2^k문제의 크기는 이진 탐색과 마찬가지로 반씩 줄어들지만, 추가되는 연산의 횟수가 다르다.
n -> (n / 2) + (c * n) -> (n / 2^2) + (c * (n / 2)) -> ...- n 크기의 문제가 (n / 2) 크기의 문제로 줄어들 때, 추가되는 연산 횟수는 n에 비례한다.
- (n / 2) 크기의 문제가 절반으로 줄어들 때, 추가되는 연산 횟수는 (n / 2) 에 비례한다.
- 왜냐하면, 점화식의 값이 바뀌어, T(n / 2) = T(n / 2^2) + c * (n / 2) 이 되기 때문이다.
문제의 크기를 계속 절반씩 줄여나가다 보면, 결국, 문제의 크기는 (n / 2^k) 이 될 것이다.
n
↓
(n / 2) + (c * n) ┐
↓ │
(n / 2^2) + (c * (n / 2)) │
↓ ├ (c * n) + (c * (n / 2)) + ... + (c * (n / 2^(k - 1)))
... │ └─────────────────────────┬─────────────────────────┘
↓ │ │
(n / 2^k) + (c * (n / 2^(k - 1))) ┘ │
↓ │
c │
│ ┌───────────────────────────┘
│ ↓
│ (c * n) + (c * (n / 2)) + ... + (c * (n / 2^(k - 1)))
│ ↓
│ c * n * (1 + (1 / 2) + ... + (1 / 2^(k - 1)) + c
│ ↑
└──────────────────────────────────────────────────────┘- 이 때, 추가되는 연산의 횟수는 이전 항의 크기에 비례하는 c * (n / 2^(k - 1)) 이다.
- 또한, 이진 탐색 때와 마찬가지로, T(n / 2^k) 의 값은 T(n / 2^k) = T(1) = c 가 된다.
- 결국, 알고리즘의 수행 시간은 c * n * (1 + (1 / 2) + … + (1 / 2^(k - 1)) + c 가 된다.
[‘14. 알고리즘 - 선택 문제 | Quick Select’](/Algorithm/Course/14. 알고리즘 - 선택 문제 | Quick Select/#3-3-2-점화식-풀이) 에서 봤듯, 1 + (1 / 2) + … + (1 / 2^(k - 1)) <= 2 다.
T(n) = c * n * (1 + (1 / 2) + ... + (1 / 2^(k - 1)) + c <= (2 * c * n) + c = O(n)결국, Quick Select 알고리즘의 최선의 경우에 대한 점화식을 풀면, T(n) = O(n) 이 된다.
참고 : 실제 교수님 강의 화면 필기 내용
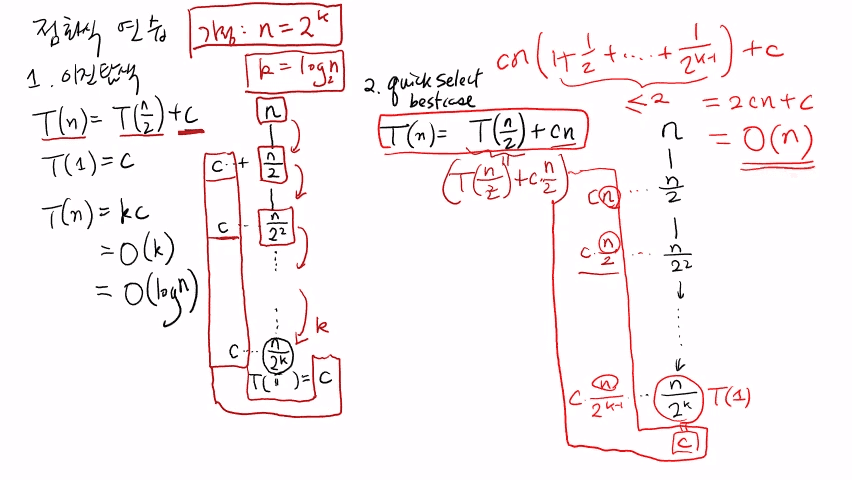
2. 이전 항의 계수가 2인 점화식
수행 시간이 T(n) = 2 * T(n / 2) + (c * n) 으로 정의되는 알고리즘이 있다고 가정해보자.
이후의 수업에서 살펴볼 정렬 알고리즘 중 일부의 수행 시간이 이러한 식으로 정의된다.
T(n) = 2 * T(n / 2) + (c * n), T(1) = c, n = 2^k2-1. 분할 정복 방식의 정렬 알고리즘
그중, Quick Sort 알고리즘의 최선의 경우(Best Case) 에 대한 수행 시간이 이에 해당한다.
참고로, Quick Sort 알고리즘은, Quick Select 알고리즘과 비슷한 방식으로 동작한다.
- Quick Sort 알고리즘도, 문제를 절반 크기의 문제로 나누기 위해, pivot 을 활용한다.
- 하지만, 이렇게 나누어진 절반 크기의 문제 두 개를 모두 푼다는 점에서 차이가 있다.
- 이 때, 문제가 나누어질 때마다, 이전 항의 크기에 비례하는 횟수의 연산이 추가된다.
여기서 잠깐,
Merge Sort 라는 정렬 알고리즘에도, 이와 비슷한 방식으로 분할 정복법이 적용된다.
(n개의 원소를 정렬하는 문제를 (n / 2) 개의 원소를 정렬하는 문제 두 개로 나눠서 푼다.)
2-2. 그림과 함께 점화식 풀기
이렇게 점화식에 대해 간단히 살펴봤으니, 이번에는 그림을 그리면서 점화식을 풀어보자.
n ┐
↙ ↘ <- (1) │
(n / 2) (n / 2) │
↙ ↘ ↙ ↘ <- (2) │
(n / 2^2) (n / 2^2) (n / 2^2) (n / 2^2) │
↙ ↘ ↙ ↘ ↙ ↘ ↙ ↘ <- (3) ├ k
(n / 2^3) ... (n / 2^3) │ │
↙ ↘ ↙ ↘ │ │
... │ │
↙ ↘ <- (k) │ │
(n / 2^k) ... (n / 2^k) ┘ │
└──────────────────────────────────┬──────────────────────────────────┘ │
count of T(n / 2^k) = 2^k = n │
k = log2(n) <-─────────┘
(1) = (c * n) * 1
(2) = (c * (n / 2)) * 2
(3) = (c * (n / 2^2)) * 2^2
(k) = (c * (n / 2^(k - 1))) * 2^(k - 1)맨 처음에, 원래 문제인 n 크기의 문제를 반으로 나누면, (n / 2) 크기의 문제 두 개가 된다.
- 이 때, 이전 항의 크기에 비례하는 값인 (c * n) 만큼의 연산을 추가로 수행해야 한다.
- 이후, (n / 2) 크기의 문제가 다시 재귀적으로 (n / 2^2) 크기의 문제 두 개로 나눠진다.
- 이전과 마찬가지로, 이전 항의 크기에 비례하는 (c * (n / 2)) 만큼의 연산이 추가된다.
- 단, (n / 2) 크기의 문제 두 개를 절반 크기로 나눴으므로, 추가 연산도 두 번 추가된다.
이렇게 만들어진 (n / 2^2) 크기의 문제는, 다시, (n / 2^3) 크기의 문제 두 개로 나눠진다.
이때도 마찬가지로, 이전 항의 크기에 비례하는 (c * (n / 2^2)) 만큼의 연산이 추가된다.
이러한 문제들은 모두, (n / 2^k), 즉, 크기가 1이 될 때까지, 계속해서 반씩 나눠질 것이다.
문제의 크기가 (n / 2^k) 으로 줄어들 땐, c * (n / 2^(k - 1)) 만큼의 연산이 추가된다.
- 이렇게, 문제의 크기가 n부터 1까지 줄어드는 동안 총 k번의 분할 작업이 수행된다.
- 그리고, 모든 분할 작업이 끝났을 때, T(n / 2^k) 의 개수는 총 2^k = n 개가 된다.
n = 2^k 이라는 가정을 통해, k = log2(n), T(n / 2^k) = T(1) = c 라는 사실을 알 수 있다.
T(n / 2^k) = c 이므로, (n / 2^k) 크기의 문제들을 푸는 데 필요한 시간은 (c * n) 이다.
2-3. 전체 수행 시간 계산하기
이렇게, 가장 작은 크기로 나눠진 n개의 문제를 전부 푸는 데 필요한 시간을 확인해봤다.
이번에는 n 크기의 문제가 (n / 2^k) 크기의 문제로 나눠지기까지 걸리는 시간을 구해보자.
- 처음에, n 크기의 문제를 (n / 2) 크기의 문제로 나누는 데 걸리는 시간은 (c * n) 이었다.
- 또, (n / 2) 크기의 문제들을 나누는 데 걸리는 시간은 (c * (n / 2)) * 2 = (c * n) 이었다.
- (n / 2^2) 크기의 문제들을 나눌 때의 시간 또한, (c * (n / 2^2)) * 2^2 = (c * n) 이었다.
결국, 모든 재귀 단계에서 문제를 나누는 데 필요한 시간은 (c * n) 이라는 것을 알아냈다.
- 가장 작은 크기의 문제를 풀 때와 문제를 반으로 나눌 때 필요한 시간은 (c * n) 이다.
- 이 때, 재귀 단계는 총 k개이므로, T(n) = k * (c * n) + (c * n) = (k + 1) * (c * n) 이다.
- 그리고, k = log2(n) 이므로, T(n) = (k + 1) * (c * n) = (log2(n) + 1) * (c * n) 이 된다.
마지막으로, 빅오 표기법으로 표현하면, T(n) = (log2(n) + 1) * (c * n) = O(n log n) 이 된다.
따라서, 이 알고리즘은 선형 시간(n) 보다 조금 더 오래 걸리는 알고리즘이라 할 수 있다.
여기서 잠깐,
- O(n log n) 에서, log2(n) 은 n에 관한 항이기 때문에, 식에서 제거해선 안 된다.
- n * log2(n), 즉, n log n 자체가 하나의 항이며, 위의 식에서는 최고차항이 된다.
- 이러한 알고리즘을. ‘선형 로그 시간에 수행되는 알고리즘’ 이라 부르기도 한다.
참고 : 실제 교수님 강의 화면 필기 내용
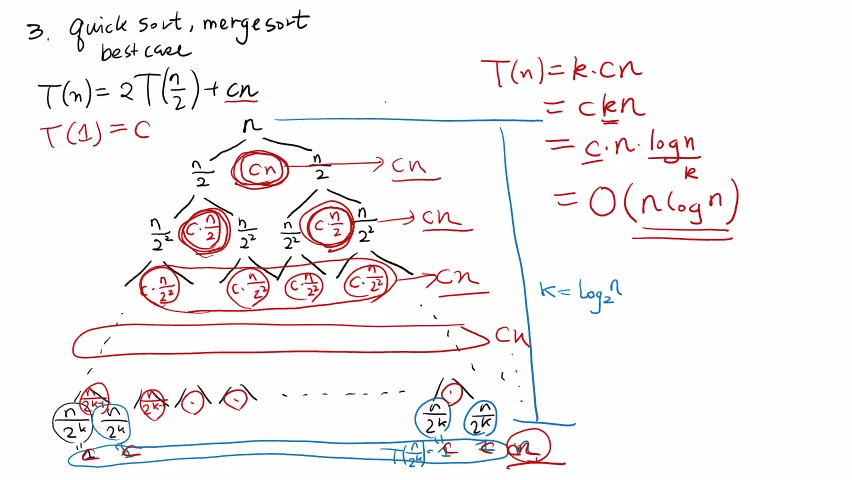
3. 이전 항의 계수가 2보다 큰 점화식
이전에 살펴봤던 Karatsuba 알고리즘의 점화식은 T(n) = 3 * T(n / 2) + (c * n) 이었다.
T(n) = 3 * T(n / 2) + (c * n), T(1) = c, n = 2^k- 문제 하나를 절반 크기의 문제 세 개로 나눠서 푸는, 재귀를 활용하는 알고리즘이다.
- 또한, 문제가 나누어질 때마다, 이전 항의 크기에 비례하는 횟수의 연산이 추가된다.
- 점화식을 보면 알 수 있듯, 이렇게 나눠진 문제들은, 다시 더 작은 크기로 나눠진다.
3-1. 그림과 함께 점화식 풀기
이번에도 마찬가지로, 알고리즘이 동작하는 방식을 그림으로 그려, 더 자세히 살펴보자.
n ┐
↙ ↓ ↘ <- (1) │
(n / 2) (n / 2) (n / 2) │
↙ ↓ ↘ ↙ ↓ ↘ ↙ ↓ ↘ <- (2) │
(n / 2^2) ... (n / 2^2) ├ k
↙ ↓ ↘ ↙ ↓ ↘ <- (3) │ │
... │ │
↙ ↘ <- (k) │ │
(n / 2^k) ... (n / 2^k) ┘ │
└───────────────────────────────┬───────────────────────────────┘ │
count of T(n / 2^k) = 3^k │
k = log2(n) <-─────────┘
(1) = (c * n) * 1
(2) = (c * (n / 2)) * 3
(3) = (c * (n / 2^2)) * 3^2
(k) = (c * (n / 2^(k - 1))) * 3^(k - 1)n 크기의 문제는 (c * n) 만큼의 추가 연산과 함께, (n / 2) 크기의 문제 세 개로 나눠진다.
- 그렇게 나눠진 문제는 다시, 추가 연산과 함께 (n / 2^2) 크기의 문제 세 개로 나눠진다.
- 물론, 해당 분할 과정에서 추가되는 연산의 수는 (n / 2) 에 비례하는, (c * (n / 2)) 이다.
결국, 문제가 (n / 2^k) 크기로 나눠질 때까지, 이러한 과정을 계속해서 반복하게 될 것이다.
- 위에서 알아낸 것을 여기에도 그대로 적용할 수 있으므로, T(n / 2^k) = T(1) = c 이다.
- 그리고, 여기서도 마찬가지로, 점화식의 재귀 단계, 즉, 분할 작업의 횟수는 총 k번이다.
이번에는 n 크기의 문제가 (n / 2^k) 크기의 문제로 나눠지기까지 걸리는 시간을 구해보자.
(c * n) + (c * (n / 2) * 3) + ... + ((c * (n / 2^(k - 1))) * 3^(k - 1))
= (c * n) * (1 + (3 / 2) + (3^2 / 2^2) + ... + (3^(k - 1) / 2^(k - 1)))
= (c * n) * (1 + (3 / 2) + (3 / 2)^2 + ... + (3 / 2)^(k - 1))
= (c * n) * ((3 / 2)^k - 1) / ((3 / 2) - 1)- 추가 연산의 횟수에 대한 식을, 식에 공통으로 들어가는 (c * n) 으로 묶어서 정리한다.
- 해당 식을 수열로 보면, 공비는 (3 / 2), 항의 개수는 k개이므로, 다시 정리할 수 있다.
3-2. 전체 수행 시간 파악하기
이제, 가장 작은 크기로 나눠진 문제들을 푸는 데 필요한 시간과 전체 수행 시간을 파악해보자.
해당 알고리즘의 경우, 모든 분할 작업이 끝났을 때, T(n / 2^k) 의 개수는 총 3^k 개다.
(c * n) * ((3 / 2)^k - 1) / ((3 / 2) - 1) + (c * 3^k)
= (c * n) * ((3 / 2)^k - 1) / (1 / 2) + (c * 3^k)
= (c * n) * ((3 / 2)^k - 1) * 2 + (c * 3^k)
= (2 * c * n) * (3 / 2)^k - (2 * c * n) + (c * 3^k)
= (2 * c * n) * (3^k / 2^k) - (2 * c * n) + (c * 3^k)
= (2 * c * n) * (3^k / n) - (2 * c * n) + (c * 3^k)
= (2 * c * 3^k) - (2 * c * n) + (c * 3^k)
= (2 * c * 3^k) + (c * 3^k) - (2 * c * n)
= (3 * c * 3^k) - (2 * c * n)
= c * 3^(k + 1) - (2 * c * n)
= c * 3^(k + 1) - (2 * c * 2^k)
= c * 3^(k + 1) - c * 2^(k + 1)
= c * (3^(k + 1) - 2^(k + 1))
= O(3^k)- 구한 식에, 가장 작은 크기의 문제들을 푸는 데 걸리는 시간을 더한 후, 식을 정리한다.
- 이 때, n = 2^k 이고, (3 / 2)^k = (3^k / 2^k) 이므로, 식을 더 간단하게 만들 수 있다.
- 이렇게 구한 식의 최고차항은 3^k 이므로, 빅오 표기법으로 표현하면 O(3^k) 이 된다.
그리고, k = log2(n) 이므로, O(3^k) = O(3^log2(n)) = O(n^log2(3)) = O(n^1.58…) 이다.
해당 알고리즘은 시간 복잡도가 O(n^2) 인 알고리즘보다 더 빠르게 동작한다는 뜻이다.
3-3. 수행 시간 비교하기
이렇게, 원래 문제를 절반 크기의 문제 세 개로 나눠서 풀 때, 수행 시간은 O(n^1.58…) 이다.
- 또한, 앞에서 살펴봤듯, 절반 크기의 문제 두 개로 나눠서 풀 때의 수행 시간은 O(n) 이다.
- 이처럼, 절반 크기로 나눠진 문제를 몇 개 풀어야 하는지에 따라서, 수행 시간이 달라진다.
Karatsuba 알고리즘과 함께 살펴봤던 분할 정복 방식의 일반적인 곱셈 알고리즘은 어떨까?
이 때, 해당 알고리즘의 수행 시간에 대한 점화식은 T(n) = 4 * T(n / 2) + (c * n) 이었다.
- 점화식을 보면 알 수 있듯, 원래 문제를 절반 크기의 문제 네 개로 나눠서 풀어야 한다.
- 즉, 절반 크기로 나눠진 문제를 Karatsuba 알고리즘보다 더 많이 풀어야 한다는 뜻이다.
- 이 때, 점화식을 풀어보면, 알고리즘의 시간 복잡도가 O(n^2) 이라는 것을 알 수 있다.
- 또, O(n^2) > O(n^1.58…) 이므로, Karatsuba 알고리즘보다 느리다는 것도 알 수 있다.
3-4. 정리
이전 방식대로 점화식을 전개해서 직접 풀어도 되지만, 이렇게 그림을 그리면서 풀 수도 있다.
- 당연한 이야기이지만, 이러한 접근 방식을 모든 점화식에 적용할 수 있는 것은 아니다.
- 하지만, 알고리즘을 개념/조직적으로 이해하는 데에 도움이 된다는 것은 큰 장점이다.
- 또, 알고리즘의 수행 과정을 직관적으로 볼 수 있어서, 동작 방식을 이해하기 쉬워진다.
참고 : 실제 교수님 강의 화면 필기 내용
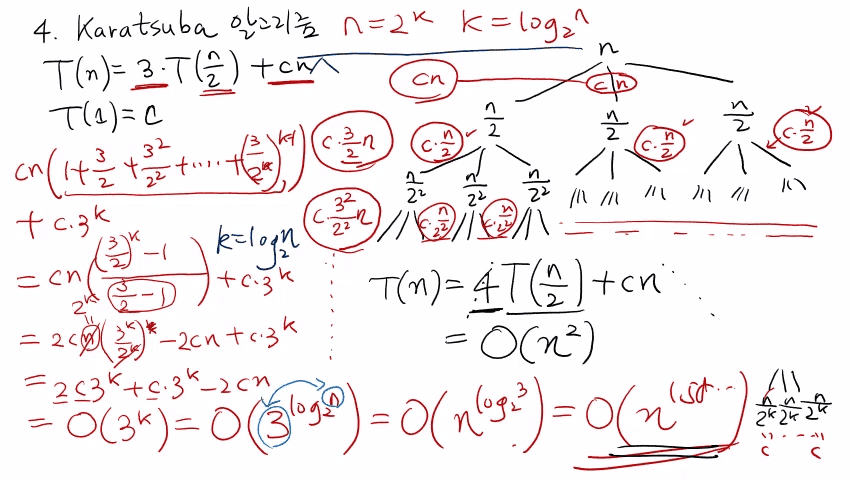
# 컴퓨터 공학# 자료 구조# 알고리즘